Here’s the thing: I have an understanding with VDARE.com’s editors that from time to time I need to write about math. This week is one of those times.
What follows is therefore math-oriented. It’s on-topic, though; at any rate, most of it is, most of the time.
The current issue of Notices of the American Mathematical Society includes a most interesting article titled “Does Diversity Trump Ability?”
The article examines a 2004 claim by economists Lu Hong and Scott Page to have proved a rigorous mathematical theorem to the effect that, to quote the title of their original paper, “Groups of diverse problem solvers can out-perform groups of high-ability problem solvers.” [In Professor’s Model, Diversity = Productivity, By Claudia Dreifus, NYT, January 8, 2008]
Referring to that paper, the Notices writer tells us:
Its publication in 2004 in the Proceedings of the National Academy of Sciences has given it credibility, and it is widely cited. Its conclusions are presented as mathematical truth. Referring to this work in his 2007 book The Difference (p. 165), Page says, “… the veracity of the diversity trumps ability claim is not a matter of dispute. It’s true, just as 1 + 1 = 2 is true.”
Under careful scrutiny, however, the paper is seen to have essential and irreparable errors.
[by Abigail Thompson, Notices of the AMS, October 2014.]
Professor Thompson—she teaches math at the University of California, Davis—proceeds to apply that careful scrutiny at 3,500-word length. She concludes:
To summarize, the paper “Groups of diverse problem solvers can outperform groups of high-ability problem solvers” contains a theorem that has neither mathematical content nor real-world applications, and a contrived computer simulation that illustrates the well-known fact that random algorithms are often effective. What the paper emphatically does not contain is information that can be applied to any real-world situation involving actual people.
The noteworthy thing here is a major mathematical journal giving over six pages to debunk Hong and Page’s diversity-boosting “theorem.”
Academic mathematicians are, in my experience, as susceptible to the siren call of Cultural Marxism as the rest of the academy. You don’t find many political dissidents in math departments.
At the very highest levels of mathematical ability there is, in fact, a tradition of political stupidity. Einstein’s partiality to Stalin is well-known. The great British mathematician G.H. Hardy (1877-1947) recorded his desire “To be proclaimed the first president of the U.S.S.R., Great Britain, and Germany”—that, in the 1940s. It wasn’t all Left-wingery, either: The tremendous French mathematical genius Augustin-Louis Cauchy (1789-1857) was the last European of any intellectual eminence to believe in the Divine Right of Kings.
My own, perhaps too charitable, opinion on this phenomenon: math at the highest levels is so difficult, so demanding of cognitive resources, that it leaves one with no mental energy to think critically about worldly matters.
However that may be, it’s encouraging to see a mathematician standing up for rigorous intellectual standards in this age of sloppy thinking, intellectual hucksterism, and ideological conformity.
Prof. Thompson writes:
Mathematicians have a responsibility to ensure that mathematics is not misused. The highly specialized language of mathematics can be used to obscure rather than reveal truth. It is easy to cross the line between analysis and advocacy when strongly held beliefs are in play.
Amen to that; although whether Hong and Page’s paper really represents “strongly held beliefs,” as opposed to a conformist desire to justify swimming along with the rest of the academic fish, is I think open to fair question.
Diversity also showed up in the Fields Medal awards this year.
The Fields Medal is an award for the highest mathematical excellence—“the Nobel Prize of math” (there is no actual math Nobel).
Every four years the International Mathematical Union holds a congress. As part of the festivities, some small number—generally two, three, or four—Fields Medals are handed out. The recipients must not be older than 40. Prior to this year’s congress, 52 medals had been awarded since the first, in 1936.
At this year’s congress, held during August in Seoul, South Korea, four Field s Medals were awarded. The awardees are here. They include the first awardee from South America, Brazilian Artur Avila, and the first ever female winner, Iranian-born Stanford Professor Maryam Mirzakhani.
Several people have asked me whether Political Correctness was at work in the award to Prof. Mirzakhani. Was the award committee thinking: “Good grief—seventy-eight years and an all-male list of winners? We’d better fix this!”
To form a judgment on that, you’d have to have a good understanding of Prof. Mirzakhani’s work and its significance in mathematics at large. I don’t have that level of understanding. Even among professional mathematicians, not many have. This is highly specialized work. To quote from the coverage in the Notices:
Mirzakhani, together with Alex Eskin and, in part, Amir Mohammedi, made a major breakthrough in understanding another dynamical system on moduli space that is related to the behavior of geodesics in moduli space. Nonclosed geodesics in moduli space are very erratic and even pathological, and it is hard to obtain any understanding of their structure and how they change when perturbed slightly. However, Mirzakhani et al. have proved that complex geodesics and their closures in moduli space are surprisingly regular, rather than irregular or fractal. It turns out that, while complex geodesics are transcendental objects defined in terms of analysis and differential geometry, their closures are algebraic objects defined in terms of polynomials and therefore have certain rigidity properties.
Hoo-kay! I know pretty much where I am there; I mean, I can locate that in the main body of mathematics, but I really have no idea whether the work done justifies a Fields. So no opinion from me on that.
What the more vulgar sort of inquirer wants to know about Prof. Mirzakhani is: How high-testosterone is she?
I am getting this particularly from friends who remember my column on the late great Emmy Noether.
![Asked to affirm that Emmy was an example of a fine woman mathematician, colleague Edmund Landau said: "I can testify that she is a fine mathematician, but that she is a woman, I cannot swear."]() Noether did not at all conform to the standards of femininity current in that time and place [1920s Germany]—nor, it has to be said in fairness to her colleagues, any other time and place. She was stocky and plain, with thick glasses and a deep, harsh voice. She wore shapeless clothes and cropped her hair. She had a rough temper, and her lecturing style was generally described as impenetrable.
Noether did not at all conform to the standards of femininity current in that time and place [1920s Germany]—nor, it has to be said in fairness to her colleagues, any other time and place. She was stocky and plain, with thick glasses and a deep, harsh voice. She wore shapeless clothes and cropped her hair. She had a rough temper, and her lecturing style was generally described as impenetrable.
[Lady of the Rings, by John Derbyshire, National Review Online, April 21st, 2005.]
Again I have no data on which to form an opinion. I haven’t heard anything like the anecdotal data that piled up around poor Emmy. Prof. Mirzakhani is a wife and mother.
![Fields Medal Winner Maryam Mirzakhani]() Photographs of her do not show any obviously high-T characteristics—no man-jaw, for example. The cropped hair is mildly suggestive; but I have a very feminine acquaintance with the same style, so I can’t read anything into it. Frankly, to my irredeemably heterosexual taste, Prof. Mirzakhani looks rather attractive.
Photographs of her do not show any obviously high-T characteristics—no man-jaw, for example. The cropped hair is mildly suggestive; but I have a very feminine acquaintance with the same style, so I can’t read anything into it. Frankly, to my irredeemably heterosexual taste, Prof. Mirzakhani looks rather attractive.
Sorry to pass wimpishly on those, but I am under the influence of Prof. Thompson’s call to proper mathematical objectivity.
And then there’s this diversity fuss about New York City’s elite specialized high schools, with math as one of the things they particularly specialize in.
I covered this on Radio Derb back in June:
New York City has of course a public-school system. Within that system are nine elite specialized high schools, in which very able kids can get a supercharged education free of charge. By New York State law, the only way to get accepted in eight of the nine is by an open competitive standard examination. (The ninth school is for music and drama; it selects by audition.)
Guess what: students from different races pass that exam at different rates. Blacks and Hispanics make up seventy percent of the relevant age group in the city; in this year’s exam they only got twelve percent of the seats in those eight schools. Non-Hispanic whites are only twelve percent of New York’s student population, they got 26 percent of the seats. Asians are only fifteen percent of the student population: they got fifty-three percent of the seats.
If you know your statistics, you’ll know that these discrepancies are going to be most prominent at the tails of the distribution. The best-known of the eight is Stuyvesant High School, and that’s also the one with the highest cutoff for admission. Stuyvesant will take in 950 freshmen this fall. Only 21 will be Hispanic; only seven will be black. Percentagewise that’s 2.2 and 0.7.
I noted that Bill de Blasio, New York City’s communist Mayor, and his schools chancellor, and the teacher union bosses, were planning to change state law to make admission to these elite public schools more “holistic.”
As Andrew Ferguson noted in his book on college admissions: “A more practical and accurate term for holistic admissions is ‘completely subjective.’”
The General Secretary Mayor and his toadies are still arguing for “holistic” admissions to Stuyvesant and the other schools (one of which, by the way, the Mayor’s son attends).
They are meeting push-back from various quarters. New York Post columnist Michael Goodwin is in the van. Congressperson Grace Meng, who represents a district in the borough of Queens, recently wrote an Op-Ed opposing the Mayor’s plan. Now the Post itself has chimed in with an editorial on the topic. (Links below).
The depressing thing is that none of these commentators displays the least trace of awareness of race realism. For goodness’ sake, how thunderingly obvious does something have to be?
Thus Goodwin:
The best charter schools aren’t closing the racial gap—they’re eliminating it. The scores of some schools dominated by black and Latino students in recent exams were tops in the state.
A mayor and a chancellor who prized excellence would be studying those examples and copying the formulas so all kids could succeed. Instead, City Hall fights success and promotes mediocrity and quotas.
[Obama’s half-hearted war on terror by Michael Goodwin; New York Post, September 21, 2014.]
“The best charter schools” have of course done no such thing. Intensive educational interventions raise test scores, though the lasting effects are disputed and there are all sorts of fudge factors—selection, expulsions—in the charter-schools equation.
Unfortunately, however, those interventions raise every group’s test scores—leaving the famous gaps intact.
You could, of course, admit only black and Hispanic students to your publicly-funded intensive educational interventions. But as a way of distributing a public good, that would be unconstitutional.
Similarly, Grace Meng:
Rather than focus on shooting the messenger [the Specialized High School Admission Test, or SHSAT] and lowering admissions standards, policymakers should focus on ensuring that all New York children are positioned to succeed academically, including on the SHSAT.
What to do?
Establish quality, universal pre-K … ?Raise awareness about the SHSAT … [Raise] access to SHSAT tutoring and test-prep … Improve our middle schools … Research ways to improve the SHSAT to ensure that it’s as fair and indicative of academic readiness as possible …
[High-school admissions test has served New Yorkers well by Grace Meng; New York Post, September 22, 2014.]
Pre-K? Pfui! Rep. Meng is way behind the curve. The New York Times has already published Op-Eds arguing for publicly-funded educational interventions at age zero.
And today the Post editorialists themselves weigh in:
There’s a better answer for minorities [i.e. better than “holistic” admissions to the elite public schools]: Rather than hurt eight good schools, why not bolster the hundreds of other school that are now failing blacks and Latinos so badly?
[Cheating NYC’s minorities, by Post Editorial Board; September 24, 2014]
Fix the schools! Why don’t we fix the schools?
Reading this stuff from intelligent, fairly sensible people of public standing, my mind goes back to that point in an Abbott and Costello routine when Costello, overcome by the level of craziness he’s encountering, howls and grabs his hat.
Finally, to really get math nostalgia out of my system, I’m going to revert to the custom I kept up for ten years when writing a monthly diary for National Review Online, of appending a mathematical brainteaser. Here we go.
My house has a small kitchen. The kitchen contains a table in one corner—that is, abutting two walls at right angles.
Since moving in 22 years ago we have lived with the previous owner’s kitchen table in that spot. This table is circular, so for 22 years stuff has been falling off the table down the corner gap and we have had to crawl under the table to retrieve it, or assign a junior member of the family so to crawl.
We have decided to get a new table for that corner. A square table is the obvious solution; but the kitchen is so small that the jutting-out corner (i.e. the one opposite the walls-corner) would be in the way, and an invitation to bang one’s thigh against it when in a hurry.
How about a quadrant, then—a quarter-circle shape? That’s OK, but they are surprisingly hard to find, and esthetically dull.
We have two kids, both now away from home; but on the occasions they are both with us, we want to sit and eat with them at the kitchen table, the family of four together.
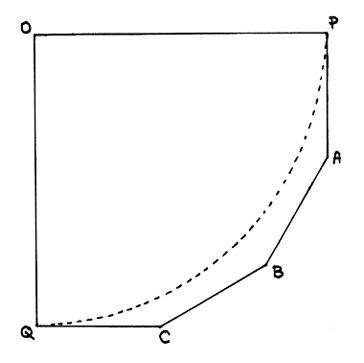
![Questions: If the long sides are 40 inches, how long are the short sides? What are the lengths of OA and OB? What is the surface area of this table? How much bigger is it than an OPQ circular quadrant (dotted line)? And: How many legs should this table have?]() My solution: A custom-made table of hexagonal shape, with two long sides OP, OQ at right angles (for the corner) and four shorter sides PA, AB, BC, CQ for us to sit at.
My solution: A custom-made table of hexagonal shape, with two long sides OP, OQ at right angles (for the corner) and four shorter sides PA, AB, BC, CQ for us to sit at.
I know a guy who makes furniture; I’m going to give him the specs and ask for a quote.
Conditions: The two long sides are of equal length; the four short sides are all of equal length; the angles at O, P, and Q are right angles, and the angles at A, B, and C are all equal.
Questions: If the long sides are 40 inches, how long are the short sides? What are the lengths of OA and OB? What is the surface area of this table? How much bigger is it than an OPQ circular quadrant (dotted line)?
And: How many legs should this table have?
Email solutions please!