Yes, the voting numbers in this election are more crooked than usual. Is there a way to quantify how crooked they are?
Math geeks have been having fun with Benford's Law. You can read up Benford's Law on Wikipedia. Here's a very short account.
Consider a big list of numbers identifying something in the real world. Wikipedia offers, quote, "electricity bills, street addresses, stock prices, house prices, population numbers, death rates, lengths of rivers, and physical and mathematical constants."
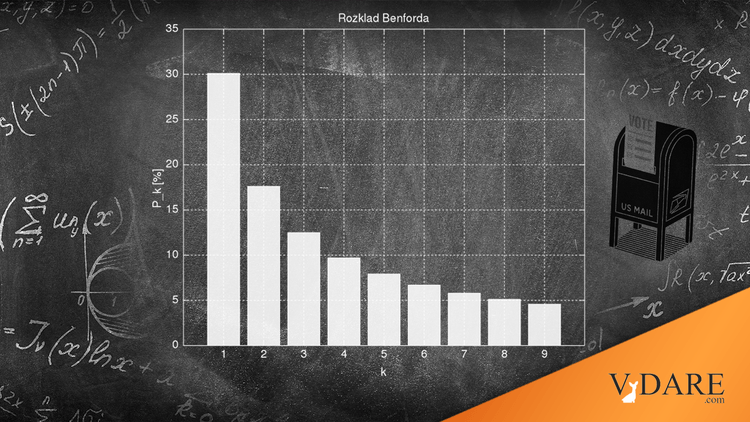
OK, you're looking at your list of house prices (say). How often is the lead-off digit in a price—the leftmost digit—how often is it a 1? Well, since it can be any one of nine digits, and there seems no reason why any digit should be favored over any other, that lead digit will be a 1 one-ninth of the time, which is to say, 11.1 percent of the time. Right?
Wrong! Benford's Law tells us that digit will be a 1 more than thirty percent of the time. At the other end, it'll be a 9 less than five percent of the time.
![]()
The distribution of first digits, according to Benford's law. Each bar represents a digit, and the height of the bar is the percentage of numbers that start with that digit.
I know: It's weirdly counterintuitive. Math can be like that. It's a real law, though, with solid theoretical explanations supporting it.
Most to the point here, it offers a way to look at a big list of numbers and see if it is, so to speak, normal. Does it obey Benford's Law? If it doesn't, there might be a good reason; but you'd want to know the reason. You'd particularly want to know if the reason was, that someone just made up the numbers, or cranked them out of a computer random-number generator.
The computer-programming website Github.com has been running the numbers for vote counts by precinct in select cities and counties. You can view results over there: Go to Github.com and search for "2020 Benford's."
The ones I've seen so far are suggestive but not, I'd say, conclusive. The biggest departures from Benford's Law show up in the Joe Biden vote counts for … uh-oh, Milwaukee and … double-uh-oh, Chicago.
Dispositive? No. Worth investigating? Definitely, if anyone's keen to do so.